抛物线的标准方程四种与抛物线定义公式
在数学的世界里,抛物线以其独特的形状和性质,成为了一个既简单又深奥的存在,它不仅仅是一种二次函数的图像,更是一种在自然科学、工程技术等多个领域中广泛应用的工具,本文将详细介绍抛物线的四种标准方程及其定义公式,并探讨其在不同领域的应用价值。
一、抛物线的定义与基本概念
抛物线(Parabola)是希腊文“para bolos”的意思,是指锥曲线中离定点(焦点)和定直线(准线)距离相等的点的轨迹,这个定义为我们理解抛物线的几何性质提供了重要的依据,抛物线的定义为:平面内到一个定点(焦点)和一条定直线(准线)的距离相等的点的轨迹,焦点不在该定直线上,这个定义使得我们可以通过点到焦点和准线距离相等的关系,来推导抛物线的方程,抛物线还有许多不同的表达形式,包括标准方程、参数方程等,每种形式都有其特定的几何意义和应用背景。
二、抛物线的四种标准方程
抛物线的标准方程有多种表达形式,常见的有以下四种:
1、y² = 2px(开口向右)
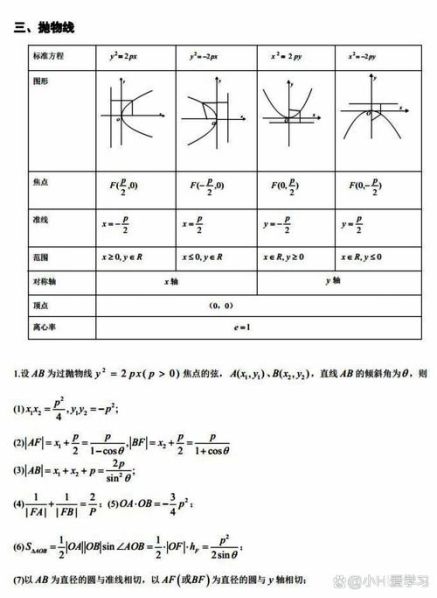
范围:x ≥ 0,y ∈ R
顶点:原点 (0,0)
对称轴:x 轴
焦点:(p/2, 0)
准线方程:x = -p/2
离心率:e = 1
2、y² = -2px(开口向左)
范围:x ≤ 0,y ∈ R
顶点:原点 (0,0)
对称轴:x 轴
焦点:(-p/2, 0)
准线方程:x = p/2
离心率:e = 1
3、x² = 2py(开口向上)
范围:y ≥ 0,x ∈ R
顶点:原点 (0,0)
对称轴:y 轴
焦点:(0, p/2)
准线方程:y = -p/2
离心率:e = 1
4、x² = -2py(开口向下)
范围:y ≤ 0,x ∈ R
顶点:原点 (0,0)
对称轴:y 轴
焦点:(0, -p/2)
准线方程:y = p/2
离心率:e = 1
四、抛物线的应用举例
1、物理学中的应用:抛物线广泛应用于投射运动的研究,例如计算物体从某高度落下后的轨迹,在忽略空气阻力的情况下,物体的质心运动轨迹为抛物线。
2、建筑学中的应用:许多现代建筑使用抛物线的几何特性进行设计,如拱桥、抛物线屋顶等,以实现力学上的稳定与美学上的优雅。
3、工程设计中的应用:在光学领域,抛物面镜的设计利用了抛物线的性质来实现平行光束的聚焦,如卫星天线的设计,汽车前照灯的设计也用到了抛物线的反射特性,确保光线聚集形成清晰的照射区域。
五、总结
抛物线不仅是数学中的一个基本概念,它在日常生活以及其他科学领域中都具有重要的应用价值,掌握好抛物线的不同标准方程及其几何性质,有助于我们在实际应用中灵活运用,通过深入了解抛物线的各种性质,可以更好地理解和解决各种工程、物理以及技术问题。
本文来自作者[侯雅琳烟]投稿,不代表臻货网立场,如若转载,请注明出处:https://www.zhenhuowang.com/changshi/202501-995.html


评论列表(3条)
我是臻货网的签约作者“侯雅琳烟”!
希望本篇文章《抛物线的标准方程四种 抛物线定义公式》能对你有所帮助!
本篇文章概览:抛物线的标准方程四种与抛物线定义公式在数学的世界里,抛物线以其独特的形状和性质,成为了一个既简单又深奥的存在,它不仅仅是一种二次函数的图像,更是一种在自然科学、工程技术等多个领...