:探索双曲线的世界
在数学的广阔天地中,双曲线以其独特的魅力和深刻的内涵吸引着无数求知者,我将带领大家走进双曲线的世界,一起探索其标准方程的奥秘,揭开这一几何图形背后的数学之美。
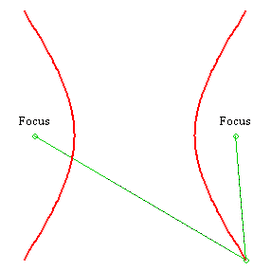
让我们从双曲线的定义开始,双曲线是一种中心在原点、开口向上或向下且有两条渐近线的曲线,它有两个分支,分别称为第一象限分支和第二象限分支,双曲线的标准方程通常表示为 ( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 ),( a ) 和 ( b ) 分别是双曲线的实轴长和虚轴长,它们之间的关系是 ( a^2 = b^2 + c^2 )。
我们探讨双曲线的标准方程如何描述现实世界中的一些现象,在物理学中,双曲线可以用来描述物体在重力作用下的运动轨迹,在天文学中,双曲线的形状可以帮助我们解释行星的运动轨迹,双曲线在音乐、绘画和摄影等领域也有着广泛的应用,比如在音乐创作中,双曲线的形状可以用于创造特定的旋律和节奏;在绘画中,双曲线的形状可以用来表现空间的深度感;在摄影中,双曲线的形状则可以创造出梦幻般的视觉效果。
让我们通过一个具体的实例来理解双曲线的标准方程,假设我们有一个双曲线 ( \frac{x^2}{4} - \frac{y^2}{3} = 1 ),这个双曲线的第一象限分支是一个椭圆,它的长轴长度是4,短轴长度是3,离心率是 (\sqrt{3}/2),这个例子展示了双曲线在不同分支下的表现,以及它在实际应用中的重要性。
在学习双曲线的标准方程时,我们不仅要掌握公式本身,还要学会如何将实际问题转化为数学模型,当我们需要计算某个物体在重力作用下沿双曲线路径运动的速度时,我们可以使用牛顿第二定律和能量守恒定律来建立方程,然后求解得到速度,这样的过程不仅锻炼了我们的数学思维能力,也让我们对物理现象有了更深入的理解。
除了理论学习,我们还应该关注双曲线在实际中的应用,随着科技的发展,双曲线的应用越来越广泛,在计算机图形学中,双曲线可以用来生成各种复杂的图形和动画效果;在医学领域,双曲线的形状可以用来设计人工器官,帮助医生进行手术;在建筑设计中,双曲线的形状可以用来设计建筑物的外观,使其更加美观和和谐,这些应用都充分体现了双曲线的实用价值和艺术魅力。
在探索双曲线的过程中,我们也会遇到一些挑战,我们需要解决一些复杂的代数方程来找到双曲线的参数 (a) 和 (b),这需要我们具备扎实的代数基础和逻辑思维能力,我们还需要学会如何将代数结果转化为几何图形,以便更好地理解和欣赏双曲线的美。
双曲线作为一种独特的几何图形,其标准方程为我们提供了丰富的数学资源和广阔的应用前景,通过学习双曲线的标准方程,我们可以更好地理解自然界的规律,也可以将数学知识应用于实际问题的解决中,让我们一起继续探索双曲线的世界,发现更多隐藏在其中
本文来自作者[采盈]投稿,不代表臻货网立场,如若转载,请注明出处:https://www.zhenhuowang.com/jyhz/202506-4059.html


评论列表(4条)
我是臻货网的签约作者“采盈”!
希望本篇文章《双曲线的标准方程课件动态 双曲线及其标准方程教案》能对你有所帮助!
本站[臻货网]内容主要涵盖:百科大全、知识汇总、百科经验、常识大全、科普解惑、经验汇总等
本文概览::探索双曲线的世界在数学的广阔天地中,双曲线以其独特的魅力和深刻的内涵吸引着无数求知者,我将带领大家走进双曲线的世界,一起探索其标准方程的奥秘,揭开这一几何图形背后的数学之美,...